Mesh Adaptation for Non-Rigid Registration

How can we apply lessons learned from adaptation for CFD and Nuclear femtography to meshing for medical images ? In particular, in the case of non rigid registration for medical images one could re-use the ideas of error-based metric construction in order to create metric than can reduce the registration error.

In the references below we presented different methods for performing non-rigid registration between medical images in the context of neurosurgery. This process is used in order to create a “mapping” between different areas of the brain before and during the operation. The initial image which is usually taken pre-operatively i.e. before a surgery is of high quality and it is used to plan the surgery. During the surgery due there is a large brain shift that occurs due to the brain tumor removal. In order to access the progress of the removal, a lower quality (but much faster) brain scan is taken during the operation¹.

The accuracy of the mapping is very important. If the tumor is not removed there is a chance that it will regrow back while removing healthy tissue puts the patient in danger. There is whole group of people from my former graduate lab² that have contributed to this research either in terms of improving the solver itself that produces the mapping or via providing a different/ faster/ more accurate discretizations (meshes) of of the image which the solver needs in order to solve the system of equations that give the mapping.

My contribution in the papers bellow was an exploration of how we can decrease the error/increase the accuracy of the mapping by performing mesh adaptation on the mesh that the solver consumes.

The input to our process is a number of landmarks $L$ between the two images provided by an expert and then a set of additional points extracted by a block matching algorithm. Also, we use a mesh $M$ generated with an Image-to-Mesh method that took into consideration only the features of the preoperative image (and not the points). The goal question now is:

How can we equi-distribute the landmarks among the mesh elements ?

Remember however! The landmarks have physical meaning and we cannot move just them. The actual questions is:

How can we arrange/adapt the mesh around the landmarks so that they are equi-distributed across the final mesh ?

The reason we are interested in the equidistribution of points is that it affect the accuracy and stability of the solver that produced the mapping.

The first transformation of this requirement to a meshing criterion came in an earlier work when they use the landmarks as a guide for mesh density. In simple terms, they tried to adapt the mesh so that there are approximately k points in each vertex-cell (i.e the union of all elements attached to a vertex). Ideally this will cause the mesh spacing to follow a density that equidistributes the point across the final mesh.

For example, in the figure below, on the left, the vertex cells of $p_1$ , $p_2$ , $p_3$ have $3$, $7$ and $5$ land marks, respectively. While on the right, by collapsing edge $p_2$ $p_1$ one can equi-distribute the landmarks. Both the vertex cells of $p_1$ and $p_2$ have now $7$ landmarks.

But, can we do better ? Notice that yet another way to interpret the above is that can define the ideal spacing of each vertex by a sphere centered at the vertex itself and having a radius equal to the distance to the $k$ closest point ! Moving the $k-1$ landmarks in any configuration does not alter the result:

But ideally we would like a different mesh right ? They could be spread around the sphere or all of them concentrated in a small area. Surely we would like a different mesh for each case…

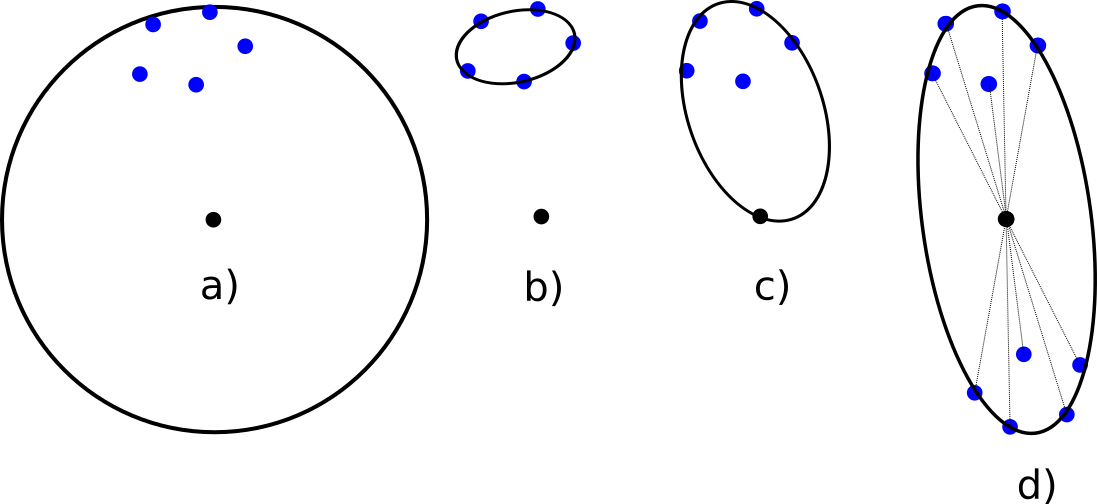
And this is where ellipsoids came into the game ! The extra degrees of freedom allow to adapt between to the shape of the distribution of the points. We also like ellipsoids because once we have them we know very well how to use them for mesh adaptation as we saw in the mesh adaptation section of the projects.

But how do we create them? How do we create the minimum (volume) ellipsoid enclosing a set of points? This question sounds very “nicely put” to not have been researched before. Indeed there is the Khachiyan Algorithm³ that can give us this ellipsoid. Notice however that we cannot just take the minimum ellipsoid of the landmarks (b). Adding just the vertex does not help either (c) because this is not centered on the vertex and we would prefer that so it matches better our experience with working with metric tensors in mesh adaptation. As a simple fix we reflect the points by the vertex which gives (d) and we use these as input to the Khachiyan algorithm.

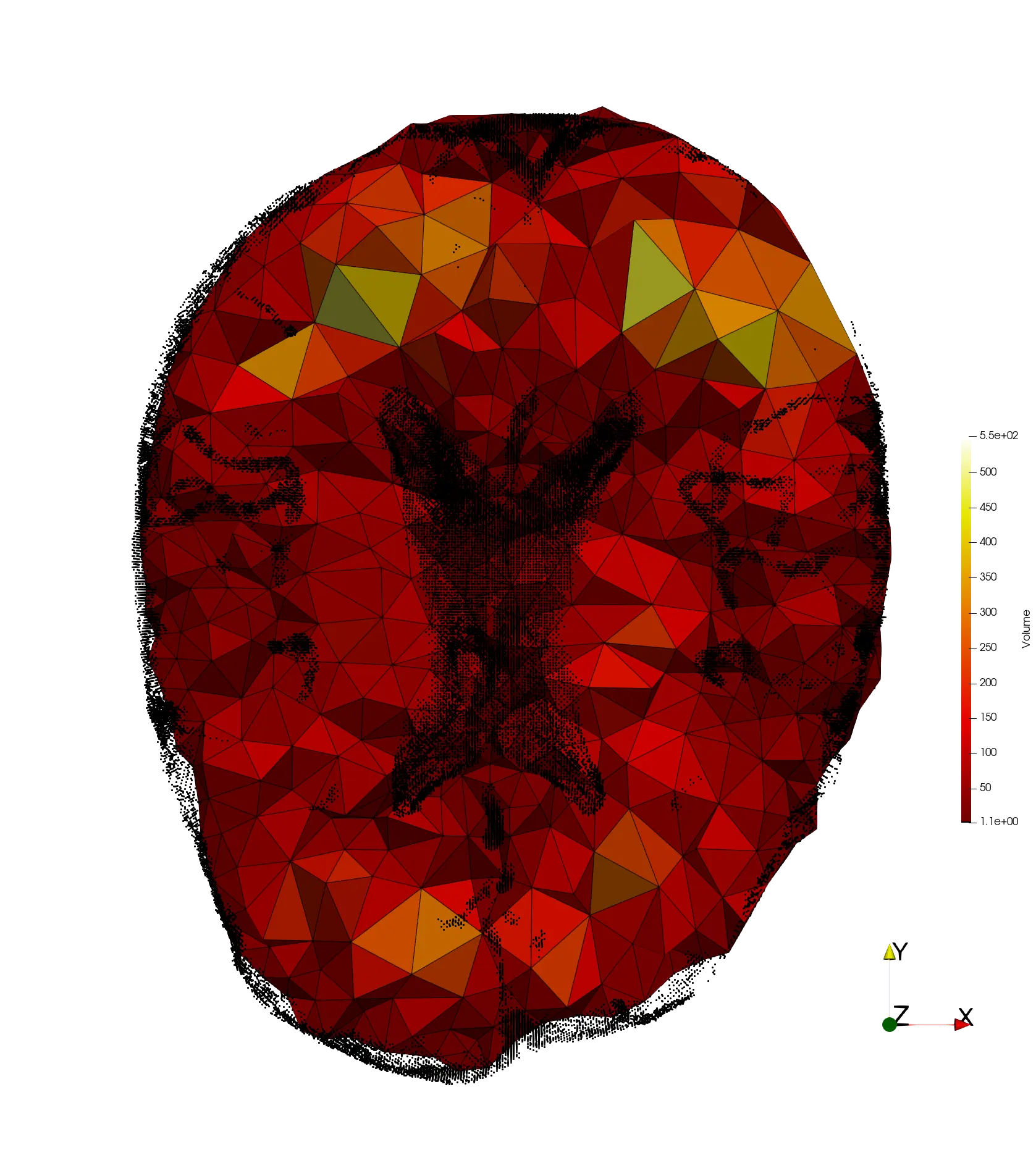
Having now a mesh at hand generated by PODM⁴ and a metric field generated as described above we pass these input to the great open source MMG3D⁵ library that adapts the mesh using the metric tensor while at the same time, respecting the boundary between the different tissues.

Looking into the final results it looks like the approach is promising but more tweaking is needed. Maybe this is a project for a future student!

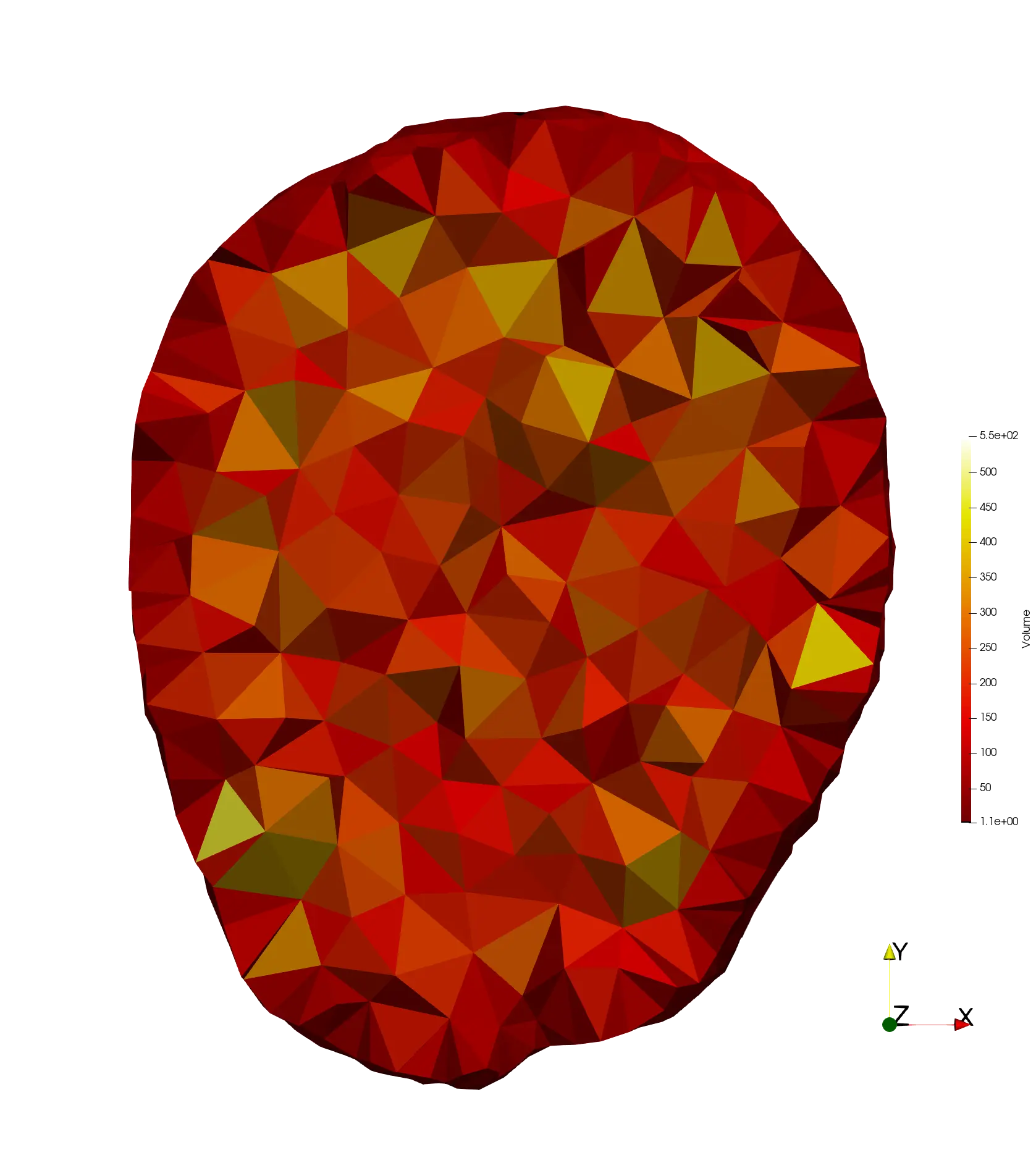
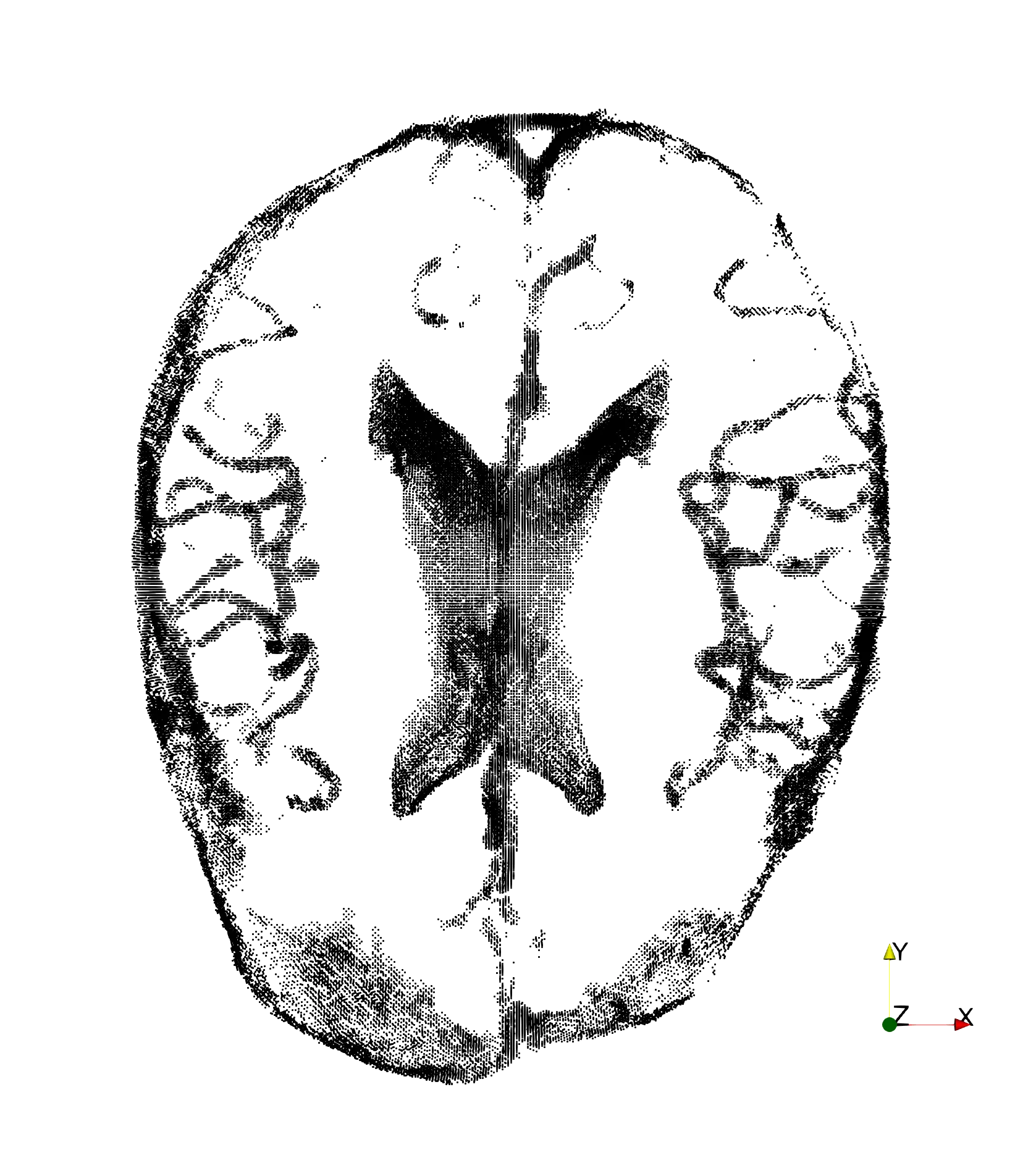
Below is the input mesh, the input landmarks and the final result.

Related papers

1. N. Chrisochoides, Y. Liu, F. Drakopoulos, A. Kot, P. Foteinos, C. Tsolakis , E. Billias, O. Clatz, N. Ayache, A. Fedorov, A. Golby, P. Black, R. Kikinis,
   "Comparison of physics-based deformable registration methods for image-guided neurosurgery,"
   Frontiers in Digital Health, 2023
   
2. F. Drakopoulos, C. Tsolakis , A. Angelopoulos, Y. Liu, C. Yao, K. Kavazidi, N. Foroglou, A. Fedorov, S. Frisken, R. Kikinis, A. Golby, N. Chrisochoides,
   "Adaptive physics-based non-rigid registration for immersive image-guided neuronavigation systems,"
   Frontiers in Digital Health, vol. 2, pp. 66, 2020